Torus Calculator Updates
9 September 2018
Initial version of the torus calculator.
10 September 2018
Added calculator descriptions of toroid terms.
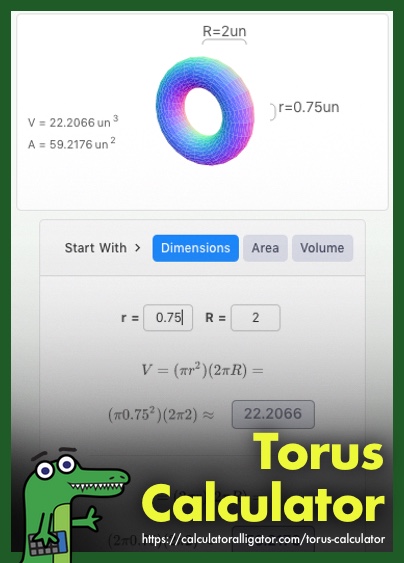
This calculator allows you to compute various measurements of a torus (or toroid) given known values.
To compute the surface area and volume of a torus in terms of it's two radii, click the 'Dimensions' button and enter the values for the major radius and the minor radius. The surface area and volume will appear in the both the torus preview and the math area, where the formulae used to make the calculations are shown. To save either the calculated surface area or volume, click the button that shows the resulting value and it will be copied to the clipboard, or click the 'Save' button to store the calculation in the calculator tape for later reference.
To calculate one of the torus's radii and volume in terms of the torus surface area, you can click the 'Area' button and supply the known values for the area. This will also display buttons with the missing torus radius and volume values that can be used to copy these calculations to the clipboard.
Finally, to calculate one of the torus's radii and area in terms of the torus's volume, click the 'Volume' button and enter the known volume.
A torus is a curved symetrical three dimensional shape that you might recognize as a donut or a bagel. You might also find torus shaped objects in the form of inner tubes or life bouys. The word torus comes from Latin where it is used generically to refer to a bump or protrudence.
You create a torus by sweeping a smaller circle perpendicularly around a path defined by a larger circle, and as such the torus is defined mathemetically by the radius of the larger circle (the major radius) and the smaller circle (the minor radius.) These two radii are shown in this torus calculator as the variables "R" and "r" respectively.
A torus has a number of interesting applications in electromagnetic phenomena, and you'll frequently encounter this shape in things like toroid magnets, chokes or other electronic components. Another application is in the structure of a prototype fusion reactor design called the tokamak, one of which is the ITER reactor being constructed in France. In this application, a torus shaped chamber is used to contain very high energy plasma in a torus shaped magnetic field to attempt to produce a sustained fusion reaction (and hopefully very inexpensive electric power.)
A torus can be considered a cylinder bent into a closed circular shape, and the math associated with the torus share some of the elegance with cylinders and circles.
Like a cylinder, is a volume defined by a radius of a circle extended over a length. In the case of a cylinder, that length is the height. For a torus, that length is the outer circle's circumference. If you were to cut a torus and straighten it out into a cylinder, you probably have some instinct that the volume of the torus is going to be similar to the volume of a cylinder. However, what about the torus's inside edge? That portion of the torus's volume is going to be "compressed" relative to our straightened out cylinder shape. Similarly, the torus's outer edge is going to contain volume that is "stretched" compared to our straightened cylindrical shape. It turns out the amount of stretching and compressing balances out perfectly, so we can take the equations for circle circumference and for cylinder volume...Unfortunately, the area of a torus doesn't have this same relationship. The equation of the area of a torus is still very elegant however...