How to Use the Pyramid Calculator

This calculator allows you to compute various measurements of a square right pyramid given a few known values.

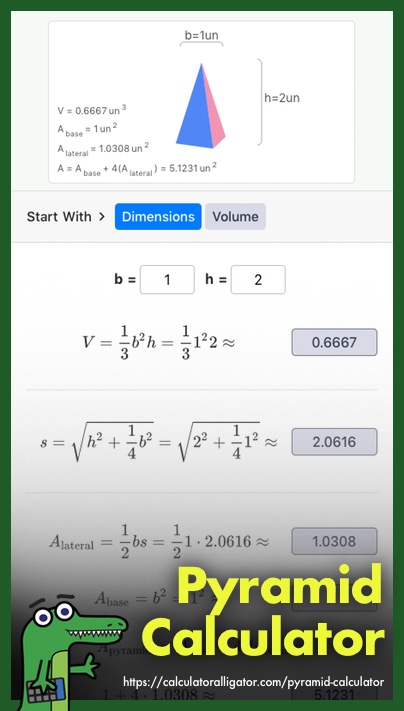
To compute the surface area and volume of a pyramid in terms of it's base dimension and height, click the 'Dimension' button and enter the known values. The surface area and volume will appear in the both the pyramid preview and the math area, where the formulae used to make the calculations are shown. To save either the calculated surface area or volume, click the button that shows the resulting value and it will be copied to the clipboard, or click the 'Save' button to store the calculation in the calculator tape for later reference.

To calculate a pyramid's dimensions and area in terms of its volume, you can click the 'Volume' button and supply the known value for the volume along with either the base or height dimension. This will also display buttons with the calculated pyramid dimensions and surface area values that can be used to copy these calculations to the clipboard.

What are Pyramids?

A pyramid is a solid geometric shape whose base is a polygon and whose sides are triagles that meet at a single apex point. We usually associate a pyramid with a shape having a square base, and therefore its sides will have the same shape and size. The Great Pyramid of Giza in Egypt has this shape. However, a pyramid can have other shapes for its base, including shapes where all the sizes are not the same length. The pyramid calculator on this page works specifically with right square pyramids, but if you read the discussion below you should have a good idea of how to calculate dimensions of more complicated pyramids.

A pyramid's apex point is traditionally located vertically above the center of the pyramid's base, creating a line segment that goes from the apex to the base's center point at a 90 degree angle. This creates a right pyramid. If the apex point is not centered over the base, the pryamid will appear to "lean" to one side or the other, and the dimensions of the triangular faces will be different from each other. Again, this pyramid calculator finds values for square pyramids.

Mathematical Properties of Pyramids

The volume of a pyramid is related to triangles in many regards. The general formula for figuring out the volume of a pyramid is to arrived at by understanding it's relationship to the area of the pyramid's base...

Equation for Volume of a Pyramid

$$V_{\mathrm{pyramid}}=<mfrac><mn>1</mn><mn>3</mn></mfrac>A_{\mathrm{base}}h$$

The surface area of a pyramid requires figuring out the surface area of all of it's surfaces, including the base. The base is easy to calculate, and we already talked about using the formula for area of a square above.

The pyramid's lateral surfaces are all triangles, and unsurprisingly we use the formula for area of a triangle to find the area of each of those surfaces.

Equation for Area of Triangle

$$A_{\mathrm{triangle}}=<mfrac><mn>1</mn><mn>2</mn></mfrac>bh$$

The base of the triangle is easy to figure out... It's the same as the base of the pyramid; that's one of the values we enter directly into the calculator. The second parameter, the triangle's height, is NOT the same as the pyramid's height pyramid. This is obvious when you think about it for a minute... The height dimension we enter into the calculator is three dimension height of the pyramid, the distance from the base's centerpoint to the apex point. That value is going to be less than the distance measured across one of the lateral faces from the base to the apex. We refer to that measurement in the calculator as the slant dimension, it's the s variable, and that value is calculated using this formula

Equation for Height of Lateral Surface

$$s=\sqrt{h^2+\frac{1}{4}{b}^2}$$

Using that value as the height of the triangle and taking the same dimension for the base, we can find the surface area of each face easily using the formula for area of a triangle. Then, to compute the total surface area we add the area of all the faces to the area . Because this is a right square pyramid, we have four faces that are the same size, so our total area is calculated like this...

Equation for Area of a Right Square Pyramid

$$A_{\mathrm{pyramid}}=A_{\mathrm{base}}+4\cdot A_{\mathrm{lateral}}$$

Pyramid Calculator Definitions

Pyramid

A pyramid is a solid geometric shape with a polygon base and triangular lateral faces that at meet at an apex point.

Lateral Surface

The triangular sides of the pyramid are refered to as lateral surfaces.

Rectangular Pyramid

A rectangular pyramid is a pyramid whose base is a rectangle.

Right Pyramid

A right pyramid's apex is centered above the pyramid's base, such that a line drawn from the apex to the base centerpoint will be perpendicular to that surface. This pyramid calculator finds values for right square pyramids.

Slant

The length from the center of one edge of the pyramid's base to the apex point. This pyramid calculator shows the slant dimension in some calculations as the variable s.

Square Pyramid

A square pyramid is a pyramid whose base is a square. This pyramid calculator finds values for right square pyramids.

Triangular Pyramid

A rectangular pyramid is a pyramid whose base is a triangle. A special case of a triangular pyramid is the tetrahedron, which is constructed entirely of equilateral triangles.

Pyramid Calculator Updates

12 September 2018

Initial version of the pyramid calculator.