How to Use the Sphere Calculator
This calculator allows you to compute various measurements of a sphere given a known value.
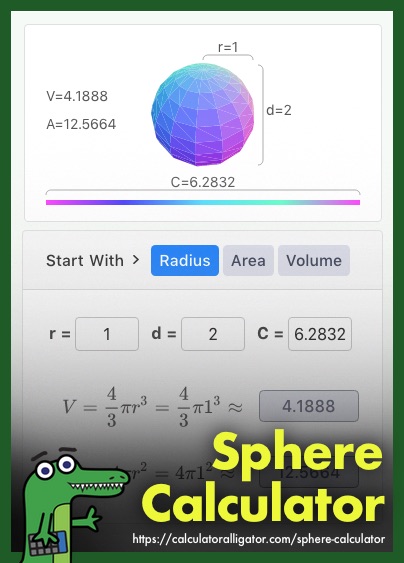
To compute the surface area and volume of a sphere in terms of its radius (or diameter, or circumference), click the 'Radius' button and enter the known value. The surface area and volume will appear in the both the sphere preview and the math area, where the formulae used to make the calculations are shown. To save either the calculated surface area or volume, click the button that shows the resulting value and it will be copied to the clipboard, or click the 'Save' button to store the calculation in the calculator tape for later reference.
To calculate a sphere's radius and volume in terms of its surface area, you can click the 'Area' button and supply the known value for the area. This will also display buttons with the calculated sphere radius and volume values that can be used to copy these calculations to the clipboard.
Finally, to calculate the radius and area in terms of the sphere's volume, click the 'Volume' button and enter the known volume.
What are Spheres?
A sphere is a curved symetrical three dimensional surface, where every point on that surface is exactly the same distance from a center origin. Because of this unique symmetry, a sphere can be defined by only a single measurement, its radius, which when swept in all three dimensions describes a mathematically closed surface. Technically, a sphere is comprised only of this surface. While a sphere encapsulates a volume, the space inside the sphere is not considered part of the sphere. Mathematicians will sometimes distinguish between a shere and its enclosed volume by referring to the later as a ball.
While perfect mathematically perfect spheres are rare in the real world, we encounter the approximation of spherical objects of all sizes regularly. The Sun, the Earth and the planets are all approximately spherical shape. Many toys you played with as a child, including balls and marbles, are spheres. And spheres are commonly used in industrial applications, for example as high-pressure fluid tanks or as components in ball bearings. Physicists consider spheres and the tineiest conceivable scales. Fundamental particles such as protons, the nucleus of a hydrogen atom, are considered to be very small spheres with a radius of roughly (0.85 × 10-15 meters.
Mathematical Properties of Spheres
The uniform geometry of a sphere makes it attractive when approximately a number of math and physics problems. The different variables relating to a sphere's geometry can be calculated from each other using a small number of formulae all related to a sphere's radius, which again is the one dimension necessary to determine a sphere's size, surface area and volume. A sphere is the most efficent shape in terms of its ratio of surface area to volume.
Like its two dimensional cousin the circle, a sphere's geometry is intertwined with the constant pi (π). An orthogonal two dimensional section through a sphere yeilds a circle, and if that section also includes the sphere's center point, the circle will be the maximum size that can be created by slicing that sphere. The radius, diameter and circumference of that circle will be the same as that circle.
However, unlike two dimensional shapes, three dimensional solids by definition have a surface area and a volume. These calculations for a sphere are also intricately related to π. For surface area, you can think of the problem in terms of how many squares with height and width dimensions equal to the radius it will take to cover the surface of the sphere...
Equation for Area of a Sphere
Similarly for the volume of a sphere, the internal space can be visualized as how many cubic radius units are needed to fill the shape...
Equation for Volume of a Sphere
Because the sphere only requires a single measurement to define its size, the volume or the radius can be used as the starting point to calculate the sphere's radius. The transformations to these equations to solve for the radius given the the volume or the area appear slightly more intimidating but are algebraically straightforward transformations of the formulae above...
Equations for Radius of a Sphere
Sphere Calculator Definitions
- Sphere
- A sphere is a three dimensional surface described by a single dimension, the sphere's radius, that when swept through three dimensions creates a closed surface.
- Antipode
- Antipodes are two opposite points on a sphere's surface. A sphere's diameter is a line segment that extends from one point on the surface, through the center point and to the opposite side of the sphere. The two points that start and end the diameter are antipodal points. Each individual point is called an antipode.
- Ball
- A solid shape consisting of all points within a sphere's volume.
- Diameter
- A sphere's diameter is a line segment that extends from one point on the sphere's surface, through the center point and terminating on an antipodal point on the opposite side of the sphere's surface. The measurement of a sphere's diameter is exactly twice its radius, and is show in the sphere calculator above as the vertical measurement labeled 'd' in the preview.
- Hemisphere
- When a sphere is divided perfectally into two halves, each half is called a hemisphere. Such a division by necessity must cross through the origin point of the sphere, so a plane that crosses the origin point will effectively divide a sphere into two hemispheres.
- Radius of a Sphere
- A sphere's radius is the distance from the center point of the sphere to any point on its surface. It is the one measurement that defines the dimensions of the sphere. The length measurement of the radius of a sphere is shown in the sphere calculator above as the horizontal measurement labeled 'r' in the preview
- Sphericity
- Sphericity is a measure of how closely a particular shape approaches that of a perfect sphere. A sphereicity of 1 is a perfect sphere with progressively smaller values indicating geometries that are less spherical.
 \
\